A rectangular plate is rotating with a constant angular speed – In the realm of mechanics, a rectangular plate rotating with a constant angular speed presents a fascinating subject that encompasses the principles of rotational dynamics, geometry, and real-world applications. This exploration delves into the intricate relationship between angular speed, torque, and moment of inertia, while examining the unique properties and applications of rectangular plates in various engineering and scientific fields.
The rectangular geometry of the plate imparts specific characteristics that influence its rotational behavior, giving rise to interesting phenomena and practical considerations. As we delve deeper into the dynamics of rotating rectangular plates, we uncover their significance in diverse areas, from gyroscopic devices to resonant systems.
Constant Angular Speed
Constant angular speed refers to the uniform rotation of an object around a fixed axis, where the angular displacement (change in angle) is constant over equal time intervals.
Examples include:
- A spinning top
- A rotating fan blade
- A CD or DVD spinning in a player
Angular speed (ω) is related to the period of rotation (T) by the equation ω = 2π/T, where ω is measured in radians per second (rad/s) and T is measured in seconds (s).
Rectangular Plate
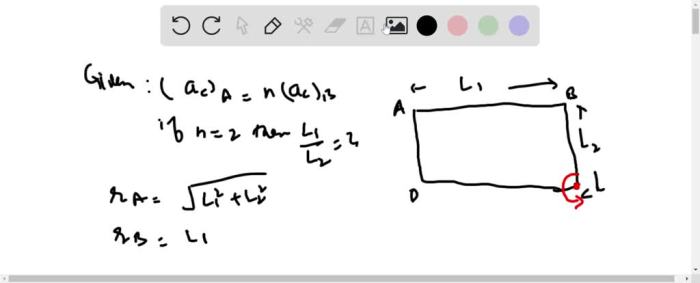
A rectangular plate is a flat, two-dimensional shape with four right angles and two pairs of parallel sides. Its geometry is defined by its length (L), width (W), and thickness (t).
Properties of a rectangular plate include:
- Area: A = L × W
- Perimeter: P = 2(L + W)
- Moment of inertia: I = (1/12) × m × (L² + W²)
The shape of a rectangular plate affects its rotation by influencing its moment of inertia, which is a measure of its resistance to angular acceleration.
Rotational Dynamics

Rotational dynamics governs the motion of rotating objects. Forces and torques acting on a rectangular plate cause it to rotate.
Key principles include:
- Newton’s second law for rotation: Στ = Iα, where Στ is the net torque, I is the moment of inertia, and α is the angular acceleration.
- Relationship between torque and angular speed: τ = Iω, where τ is the torque and ω is the angular speed.
Analyzing these relationships allows for the prediction and control of a rotating rectangular plate’s motion.
Applications: A Rectangular Plate Is Rotating With A Constant Angular Speed

Rectangular plates rotating with constant angular speed find applications in:
- Turntables
- Propellers
- Gyroscopes
- Industrial machinery
Design considerations include:
- Material properties
- Rotational speed requirements
- Torque requirements
Advanced Concepts
Advanced concepts related to the rotation of rectangular plates include:
- Gyroscopic effects: The tendency of a rotating object to resist changes in its orientation.
- Resonance: The tendency of a rotating object to vibrate at specific frequencies.
- Stability: The ability of a rotating object to maintain its rotational motion.
Exploring these concepts opens up avenues for further research and innovation in the field of rotating systems.
Questions Often Asked
What is the relationship between angular speed and period of rotation?
Angular speed and period of rotation are inversely proportional. A higher angular speed corresponds to a shorter period of rotation, and vice versa.
How does the shape of a rectangular plate affect its rotation?
The rectangular shape of the plate influences its moment of inertia, which in turn affects its resistance to angular acceleration. A rectangular plate with a larger moment of inertia will rotate more slowly for the same applied torque.
What are some applications of rectangular plates rotating with constant angular speed?
Rotating rectangular plates find applications in various devices and systems, including gyroscopes, motors, fans, and centrifuges.